Slides d'un cours d'ouverture sur les réseaux de neurones.

Apprentissage supervisé : Classification

Exemple Prenons un exemple concret : on cherche à déterminer si un patient est atteint d’une maladie à partir de sa tension artérielle et sa fréquence cardiaque.

• \(\mathcal{X}=\mathbb{R}^{3}\) car il y a 2 features numériques.

• \(\mathcal{Y}=\{Sain,Malade\}\)

• \(\mathcal{D}\) représente les données médicales de différents patients \(\{((11.2,132.4),Sain),\; ((15.4,112.8),Malade),\dots\}\)

• \(\mathcal{F}\) peut être vu comme un robot médecin : on lui donne en entrée les données physiologiques du patient et il doit nous répondre si celui ci est malade ou non. Un bon modèle devrait bien se comporter sur les données mises à disposition.

Approche probabiliste

Autant pour des raisons pratiques que mathématiques, on préfère ne pas sortir un diagnostic binaire Sain/Malade mais plutôt une probabilité.

On souhaite trouver un modèle \(\mathcal{F}:\mathbb{R}^{2}\to[0,1]\) qui donne la probabilité d’être malade à partir des données physiologiques \(X\), les features que nous notons par la suite \((x_{1},x_{2})\).

Régression logistique

Un exemple de modèle de classification binaire est la régréssion logistique : \(\mathcal{F}_{a,b,c}(X)=\mathcal{F}_{a,b,c}(x_{1},x_{2})=\frac{e^{ax_{1}+bx_{2}+c}}{1+e^{ax_{1}+bx_{2}+c}}\)

• \(\mathcal{F}_{a,b,c}\) s’écrit comme la composée d’une forme affine \((x_{1},x_{2})\to ax_{1}+bx_{2}+c\) suivie de la fonction sigmoïde \(\sigma :z\to\frac{e^{z}}{1+e^{z}}\) qui "fait rentrer" \(\mathbb{R}\) dans \([0,1]\) de sorte à modéliser une probabilité.

• plus \(ax_{1}+bx_{2}+c\) est positivement grand (resp. négativement grand) plus la probabilité est proche de 1 (resp. proche de 0).

• la probabilité d’être sain vaut \(1-\mathcal{F}_{a,b,c}(x_{1},x_{2})=\frac{1}{1+e^{ax_{1}+bx_{2}+c}}\)

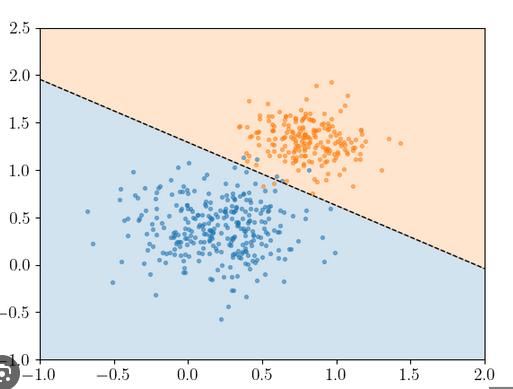
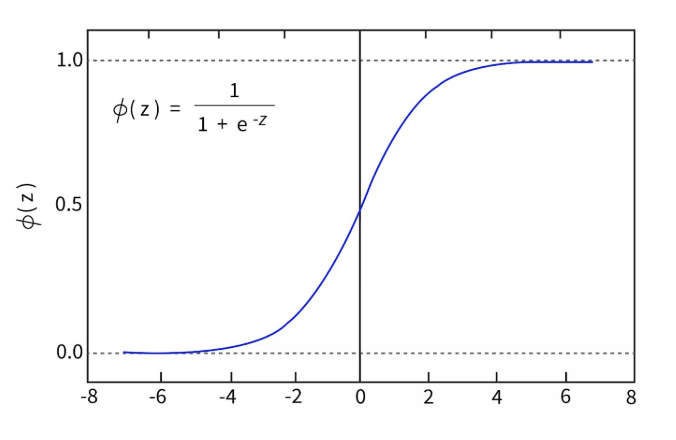
Maximiser la vraisemblance / Maximum likelihood Comment choisir les paramètres a,b,c ? Qu’est ce qu’un bon modèle? Celui qui maximise la vraisemblance des données observées (maximum likelihood estimation en anglais) :

\[\mathcal{L}(a,b,c)=\prod_{y_{i}=Malade}\mathcal{F}_{a,b,c}(X_{i})\times \prod_{y_{i}=Sain}(1-\mathcal{F}_{a,b,c}(X_{i}))\]

En résumé :

• On choisit un type de classifieur (ici régression logistique) qui dépend d’un certain nombres de paramètres à ajuster (ici a,b,c).

• La vraisemblance \(\mathcal{L}\), la probabilité d’observer les données à disposition \(\mathcal{D}\), dépend directement de ces paramètres.

• Maximiser la vraisemblance donnera le meilleur modèle.

Descente de gradient : une dimension Lorsqu’on souhait trouver un extremum (maximum ou minimum) d’une fonction différentiable on regarde les points où s’annule son gradient. Il est parfois difficile de résoudre cette équation, la descente de gradient permet de s’en approcher.

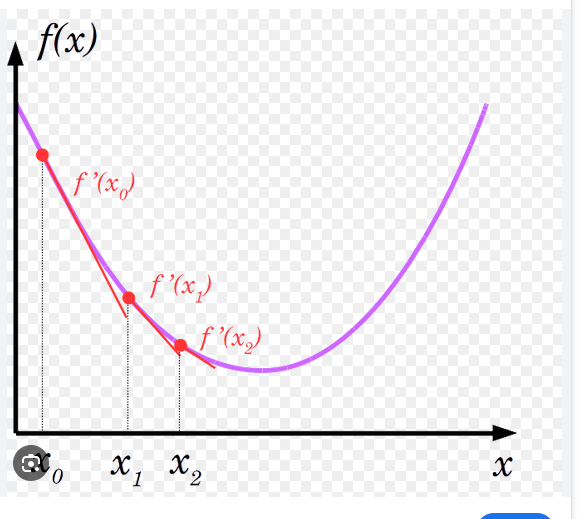
Pour une fonction \(f:\mathbb{R}\to\mathbb{R}\) c’est assez simple : à partir d’un point, on dispose de deux directions (gauche ou droite) vers lesquelles se déplacer pour augmenter/diminuer la valeur de la fonction et le signe de la dérivée nous guide.

Descente de gradient : multiples dimensions Pour une fonction \(f:\mathbb{R}^{n}\to\mathbb{R}\) on a maintenant une cercle entier de directions vers lesquelles se déplacer et le gradient \(\nabla f\) pointe celle vers laquelle la fonction croît le plus localement.

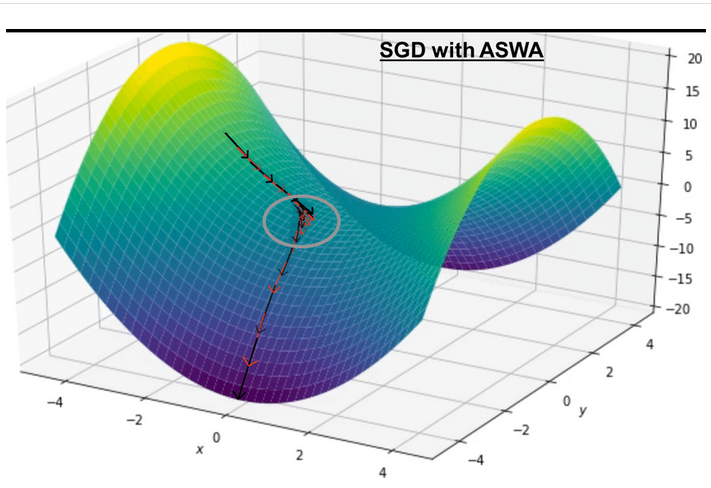
Pensez à une paysage montagneux : le relief peut s’interpréter comme une fonction hauteur du plan et le gradient en un point correspond à la direction où la pente est la plus raide.

Bilan

• La régression logistique modélise une probabilité : étant donné un couple \((x_{1},x_{2})\) représentant la fréquence cardiaque et la tension artérielle on modélise la probabilité d’être malade par \(\mathcal{F}_{a,b}(x_{1},x_{2})\).

• La vraisemblance des données observées \(\mathcal{L}\) est une fonction différentiable des paramètres.

• Bien qu’on ne puisse pas trouver un maximum explicite par \(\nabla \mathcal{L}=0\) on peut s’en rapprocher pas à pas en suivant le gradient \(\nabla \mathcal{L}\).

Réseaux de neurones : inspiré du cerveau humain

Le cerveau humain est composé de neurones et de connexions neuronales

Lors d’une activité cérébrale, un neurone reçoit un signal électrique plus ou moins intense et le propage à ses voisins lui même avec plus ou moins d’intensité.

Le cerveau : un graphe géant

Notre cerveau est en réalité un graphe pondéré géant (environ 100 milliards de sommets).

Un tel graphe peut modéliser une multitude de fonctions que vous utilisez chaque jour : lorsque vous regardez une image avec un chat dessus, vos neurones récepteurs s’allument avec plus ou moins d’intensité. Ils propagent le signal électrique dans le graphe pondéré jusqu’à un neurone final qui s’allume si un chat est présent sur l’image.

Deep Neural Networks En reprenant le problème de classification binaire Sain/Malade, on pourrait remplacer la régression logistique par un (petit) réseau de neurones.

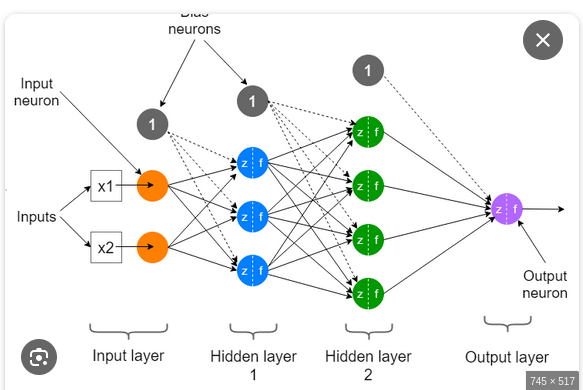
• Les 2 neurones oranges à gauche correspondent aux features en entrée \((x_{1},x_{2})\).

• Les 3 neurones bleus s’obtiennent par combinaisons affines des neurones oranges \(y_{i}^{1}=\sum_{j=1}^{3}a_{ij}^{1}x_{j}+b_{i}^{1}\) avec \(i\in\{1,2,3\}\).

• Les 4 neurones verts s’obtiennent par combinaisons affines des neurones bleus \(y_{i}^{2}=\sum_{j=1}^{3}a_{ij}^{2}y_{j}^{1}+b_{i}^{2}\) avec \(i\in\{1,2,3,4\}\).

• Le neurone de sortie violet s’obtient par combinaison linéaire des neurones verts \(y^{3}=\sum_{j=1}^{4}a_{ij}^{3}y_{j}^{2}+b^{3}\) suivi de la fonction sigmoïde afin d’avoir une probabilité.

Fonctions d’activation Le problème ici est que prendre des combinaisons affines de combinaisons affines donnera ... une combinaison affine. C’est comme multiplier plusieurs matrices avec des tailles compatibles : on obtient quand même une matrice à la fin.

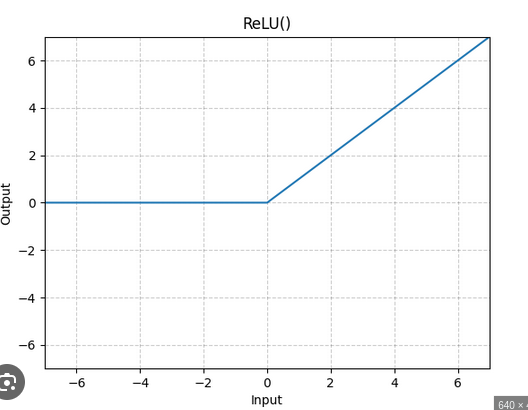
Toujours en s’inspirant de notre système nerveux, on décide d’annuler un signal négatif : si la combinaison affine des neurones précédents reçu est négative alors on éteint le neurone qui transmettra 0, ce qui revient à appliquer la fonction ReLU (Rectified Linear Unit) : \(x\to max(x,0)\).

Il existe d’autres fonctions non linéaires qu’on peut appliquer aux neurones intermédiaires, en pratique ReLU marche bien.

En résumé :

• Il y a une couche d’entrée (input layer) avec un neurone par features.

• De multiples couches intermédiaires (hidden layers) de taille variable.

• Chaque neurone d’une couche reçoit une combinaison affine du signal des neurones de la couche précédente et applique une fonction d’activation non linéaire (ici ReLU) pour générer son propre signal.

• Le dernier neurone se comporte comme la régression logistique : il reçoit une combinaison affine de la dernière couche cachée et applique la fonction sigmoïde pour modéliser la probabilité désirée.

Descente de gradient : again

Notre modèle dépend ici de \(2\times 3+3+3\times4+4+4\times1+1=30\) nombres et, comme pour la régréssion logistique, la vraissemblance \(\mathcal{L}\) est donc une fonction dépendant de 30 paramètres à maximiser.

La vraissemblance \(\mathcal{L}:\mathbb{R}^{30}\to[0,1]\) s’écrit encore comme la composée de fonctions différentiables. Il est encore plus compliqué de résoudre \(\nabla\mathcal{L}=0\) mais on peut calculer son gradient et s’approcher d’un optimum par descente.

Les pièges tendus par la non convexité

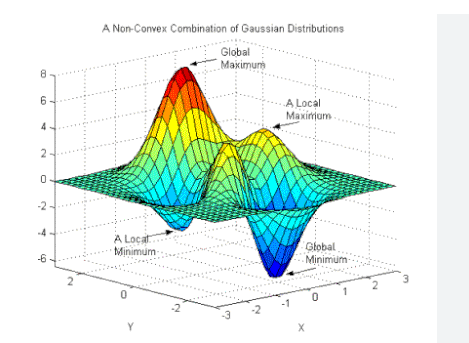
Notez que, contrairement à la régression logistique, \(\mathcal{L}\) peut être très complexe, en particulier non convexe et il est possible d’atterir dans des extrema locaux non optimaux.

Bilan

• On choisit la forme de notre réseau : combien de couches intermédiaires, combien de neurones par couche et la fonction d’activation.

• La forme du réseau choisi nous donne un certain nombres de paramètres : chaque neurone reçoit la somme pondérée des signaux des neurones de la couche précédente plus un terme constant. Les paramètres sont les poids intervenant dans cette pondération ainsi que les termes constants, appelés biais.

• La fonction de vraisemblance dépend des paramètres précédents, des algorithmes d’optimisation permettent de chercher les valeurs qui la maximisent afin d’avoir un modèle performant.

Avantages et Inconvénients

Avantages

• Universalité : n’importe quelle fonction peut être approchée raisonnablement par un réseau de neurones moyennant assez de couches et de neurones par couche.

Inconvénients

• Comme le modèle est très complexe il est sujet au surapprentissage, il vaut mieux avoir beaucoup d’échantillons.

• L’optimisation est très gourmande en calcul. En pratique on ne peut calculer le gradient de la vraisemblance sur le jeu de données entier. On sélectionne un sous ensemble d’échantillons, on calcule le gradient de la vraisemblance sur la sous population, on incrémente les paramètres et ainsi de suite. La taille du sous échantillon s’appelle le batch size.

• Pour une régression logistique on peut regarder comment telle feature influe sur le résultat en regardant le coefficient associé. Par leur complexité, les réseaux de neurones sont plus difficiles à comprendre.

Le cas des images : beaucoup de features Bien que, dans la théorie, les réseaux de neurones précédemment évoqués soient capables d’approximer n’importe quelle fonction, dans le cas d’une image, la taille du réseau est titanesque rendant l’apprentissage impossible en pratique.

Prenons le cas d’une image avec \(512\times 512\) pixels soit \(512\times 512\times 3=786432\) features. En rajoutant une seule couche avec le même nombres de neurones on obtient déjà \(786432\times786432\) connexions à trouver soit \(\simeq 6.2\times 10^{11}\).

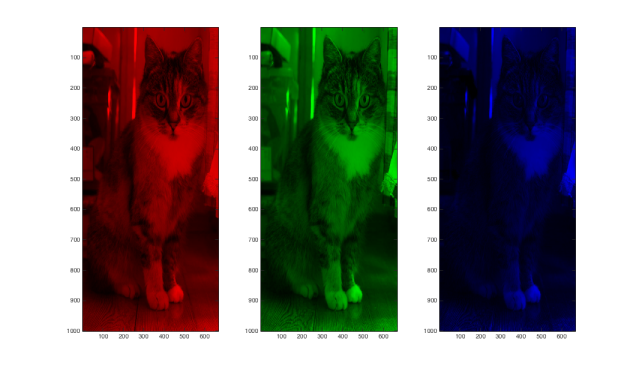
En comparaisaon, Xception, un réseau de neurones très performant pouvant distinguer 1000 objets avec une précision de 80%, n’a qu’environ 20 millions de paramètres.

Comment reconnaître un chat sur une image? Prenons le problème de classification binaire suivant : détecter si oui ou non un chat est présent dans l’image.

• Comment avez vous reconnu le chat sur l’image ci dessus ? Parcequ’il a une tête de chat, une queue de chat et des petites patounes de chat.

• Comment avez vous reconnu la tête du chat? Parcequ’elle a des yeux, un museau et des oreilles de chat.

• Comment avez vous reconnu les yeux du chat ? ...

La pyramide des caractéristiques On comprend dès lors la structure pyramidale des caractéristiques qui nous permettent de le reconnaître. Il serait plus pratique d’avoir accès aux informations "présence de queue", "présence de museau" mais l’image est stockée sous un format peu interprétable par l’ordinateur i.e. la dose de rouge/bleu/vert pixel par pixel.

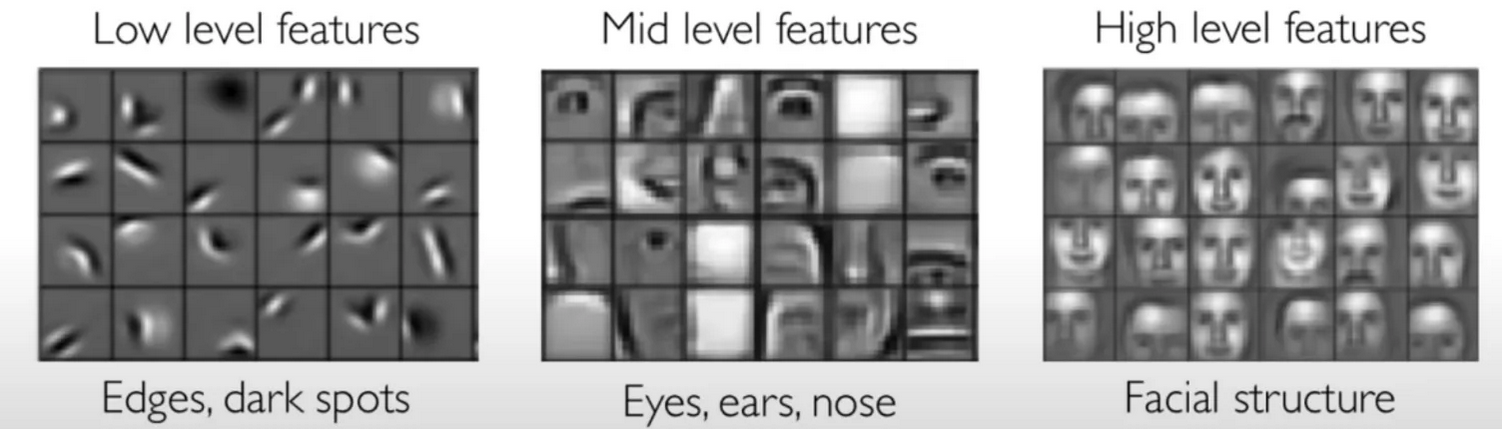
Il faudrait ici faire le chemin inverse : essayer de détecter des caractéristiques simples à partir de cette information brute comme des lignes, des segments pour en déduire des plus complexes comme des formes géométriques élémentaires et ainsi de suite jusqu’à être capable de détecter des éléments essentiels comme la tête et la queue.

La vision par ordinateur avant le deep learning

Regardons sur une image simplissime (pas de couleur et de taille \(6\times 6\) pixels) représentant une frontière verticale. En glissant le filtre de taille \(3\times 3\) on est capable de localiser la frontière verticale dans l’image.

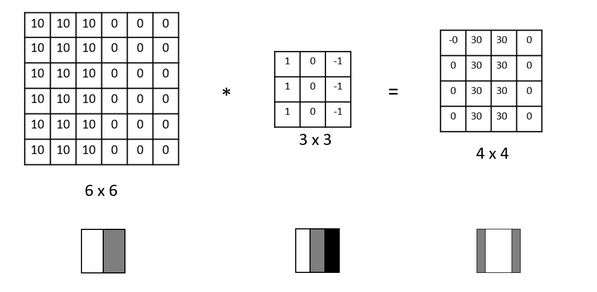
Une animation est disponible ici:

Trouver les segments (Edge detection) Admirez le résultat sur une vraie image.

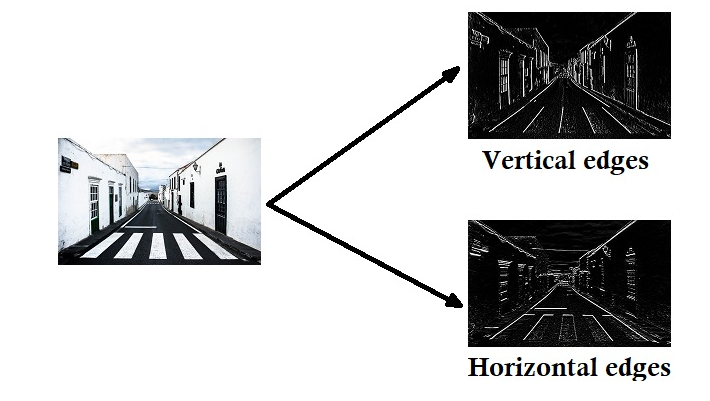
Remarquez que cette fois ci, l’image en entrée n’était pas en noir et blanc. Le filtre de convolution utilisé possède trois axes, c’est un "cube de nombres".

https://makeagif.com/gif/convolution-rgb-image-mT1rkl

Des convolutions et du Pooling En appliquant un filtre de dimension \(3\times3\times 3\) à notre image de dimension \(H\times W\times 3\) on a produit deux autres "images" où la valeur d’un pixel mesure la présence d’un segment (horizontal ou vertical) soit une "image" finale de taille \(H\times W\times 2\).

En réitérant sur la nouvelle image on peut, avec des filtre adaptés, détecter la présence de coins, puis de triangles etc... on obtient des "images" ou plutôt feature map indiquant la présence de caractéristiques de plus en plus sophistiquées.

Qui dit plus compliqué dit plus gros et il convient de réduire la résolution : soit en sautant des pas lors de la convolution, soit en appliquant du Pooling (réduire la résolution spatiale en prenant la moyenne sur une fenêtre).

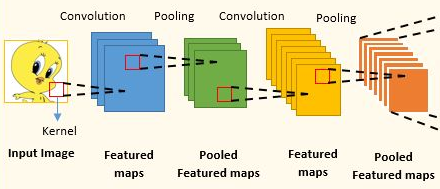
• On part de notres image RGB de dimension \(H_{1}\times W_{1}\times d_{1}\) avec \(D_{1}=3\)

• On applique \(D_{n+1}\) filtres de dimensions \(h_{n}\times k_{n}\times D_{n}\) au n-ième feature map de dimensions \(H_{n}\times W_{n}\times D_{n}\) pour obtenir un feature map de dimension \(H_{n}\times W_{n}\times D_{n+1}\). On a introduit \(h_{n}\times k_{n}\times D_{n}\times D_{n+1}\) paramètres.

• On rajoute un terme constant par filtre, soit \(D_{n+1}\) paramètres et on applique ReLU pour ne pas avoir un modèle linéaire.

• On effectue un Pooling pour diminuer la résolution spatiale pour produire le (n+1)-ième feature map de dimensions \(H_{n+1}\times W_{n+1}\times D_{n+1}\).

• On rétière (b)-(c)-(d)

De la feuille au spaghetti L’information est toujours organisé sour la forme de tenseurs à 3 axes \(H_{n}\times W_{n}\times D_{n}\) les deux premiers étant spatiaux et le dernier en profondeur : c’est lui qui encode les caractéristiques au stade n.

Au fil des étapes, les caractéristiques détectées sont de plus en plus complexes et occupent une part importante de l’espace 2D, les résolutions spatiales \(H_{n}\) et \(W_{n}\) diminuent au profit de \(D_{n}\) qui augmente : leur présence est encodée dans un vecteur de plus en plus long.

Convolutional Neural Networks Une fois que les objets détectés par le dernier feature map de dimension \(H_{n}\times W_{n}\times D_{n}\) sont considérés comme assez sophistiqués on a deux possibilités

• aplatir notre dernier feature map de dimensions en un vecteur de taille \(H_{n}\times W_{n}\times D_{n}\)

• faire la moyenne suivant les deux axes spatiaux pour obtenir un vecteur de taille \(D_{n}\): si la feature apparaît dans l’image, elle restera présente dans la moyenne et sa présence sera encodée dans le vecteur.

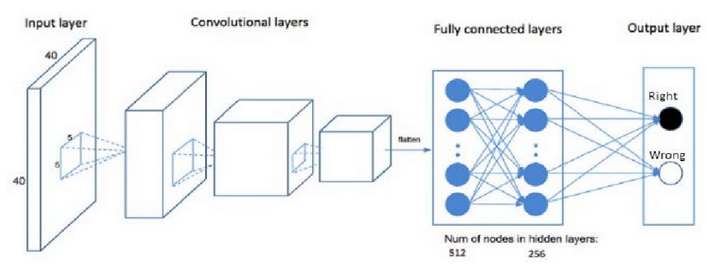
On peut ensuite continuer comme avec un réseau de neurones classique, en rajoutant des layers jusqu’à sortir la probabilité.

Vous avez un propotype de Réseau de Neurones Convolutionnel ou Convolutional Neural Network.

Bilan

• Dans le choix de notre architecture, en plus du nombre d’étapes intermédiaires et du nombre de filtres choisis, on a liberté de choisir leurs dimensions spatiales.

• Il faut aussi décider où placer du pooling pour diminuer la résolution spatiale du feature map ainsi que la baisse de résolution (en général on divise par 2).

• Avant l’arrivée des CNNs, les filtres étaient construits à la main comme le déctecteur de segments. Dans le cas des CNNs, la maximisation de la vraisemblance (qui dépend des paramètres présents dans les filtres) guide le réseau dans la recherche de features pertinentes à détecter.

• Bien qu’il soit toujours compliqué d’expliquer clairement l’apprentissage du réseau, on peut regarder la carte d’activation d’une feature sur une image donnée pour la reconnaître.

Comprendre la réponse du réseau : Saliency Map En pratique, les caractéristiques que le réseau s’est entraîné à détecter pour bien classifier les échantillons vus peuvent rester difficilement interprétable car on regarde une partir du feature map, une coordonnée. Pour comprendre où le réseau regarde on peut visualiser le Saliency Map : ce sont les régions dans l’image qui influent le plus sur la décision.

Sur une image donnée, une fois les paramètres fixés, la probabilité sortie par le réseau s’écrit comme la composée de fonctions différentiables. On peut donc calculer le gradient vis à vis des pixels d’entrée et regarder où celui-ci est grand, c’est à dire les pixels où un petit changement affecterait la réponse.

Chien ou Loup ? Ça dépend de la neige...

Cet outil nous permet de débuguer des réseaux qui ont mal appris, ceux qui se basent sur des mauvaises features.

Une différence cruciale et essentielle : le partage de paramètres

Une différence importante par rapport aux réseaux de neurones profond est la notion de partage de paramètres : dans un réseau classique, chaque neurone peut traiter le signal reçu indépendamment de ses voisins dans la même couche.

Dans le cas des CNN, un même filtre va être appliqué à différents endroits d’un feature map pour générer le suivant : le résultat varie car l’entrée varie mais la manière de transformer l’information, c’est à dire la convolution avec le filtre, est constante.

En plus de réduire drastiquement le nombre de paramètres, ce procédé possède une propriété sympathique : l’invariance par translation. Une feature, peu importe sa position, sera générée de la même manière peu importe sa position dans l’image.

Classification parmi plus de deux classes Par souci de simplicité, j’ai présenté un problème de classification binaire. Il est facilement possible de classifier un objet parmi de multiples catégories. Supposons maintenant que l’on souhaite classifier des objets présentants m features numériques parmi n classes.

Soit \(W\in\mathcal{M}_{n,m}(\mathbb{R})\) et \(b\in\mathbb{R}^{n}\) et \(X\in\mathbb{R}^{m}\) un échantillon à classer. On passe du vecteur \(WX+b \in\mathbb{R}^{n}\) à une distribution de probabilité sur \(\{1,2,\dots,n\}\) en appliquant la fonction exponentielle à chaque coordonnée pour obtenir un vecteur à coordonnées strictements positives puis en divisant par la somme des coordonnées.

Softmax

Comme pour la régression logistique, plus la j-ième coordonnée de \(WX+b\) est grande plus la probabilité que \(X\) appartienne à la classe j est élevée. Cette opération s’appelle le softmax :

\[\begin{pmatrix} x_{1} \\ \dots \\ x_{n} \end{pmatrix} \to \begin{pmatrix} \Sigma_{j}a_{1j} x_{j} +b_{1}\\ \dots \\ \Sigma_{j}a_{nj} x_{j} +b_{n} \end{pmatrix} \to \begin{pmatrix} \exp(\Sigma_{j}a_{1j} x_{j} +b_{1})\\ \dots \\ \exp(\Sigma_{j}a_{nj} x_{j} +b_{n}) \end{pmatrix}\] \[\to \frac{1}{\Sigma_{i}\exp(\Sigma_{j}a_{ij} x_{j} +b_{i})} \begin{pmatrix} \exp(\Sigma_{j}a_{1j} x_{j} +b_{1})\\ \dots \\ \exp(\Sigma_{j}a_{nj} x_{j} +b_{n}) \end{pmatrix} \ \]

Introducing ... VGGNet ! En appliquant ce procédé aux neurones de la dernière couche on obtient un classifieur d’images : sous vos yeux, VGGNet (envrion 150 millions de paramètres, capable de distinguer 1000 objets ) :

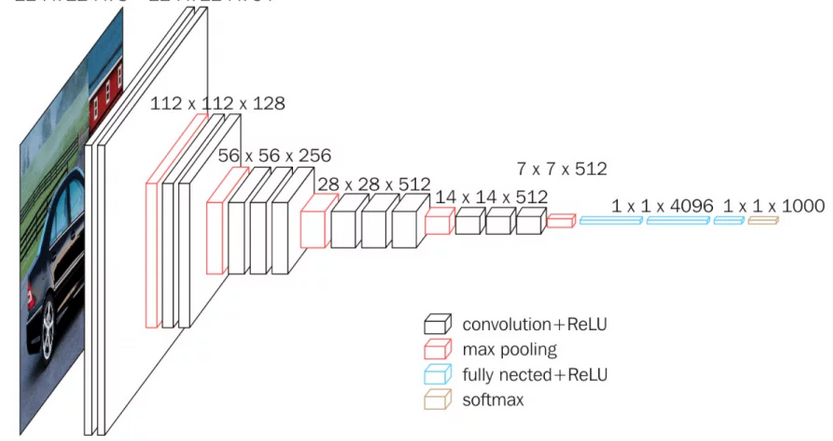
D’autres tâches

• Si plutôt que classifier un objet on souhaitait inférer une quantité numérique, disons estimer le prix d’une maison à partir d’une photo,faire une régression, on peut ajuster la structure du CNN. On enlève le layer softmax et pour sortir une combinaison linéaire des derniers neurones. Un bon modèle devrait sortir une quantité proche de la quantité observée sur les données, on remplace la fonction vraisemblance à maximiser par une fonction erreur à minimiser.

• Les CNNs sont capables d’effectuer des tâches encore plus complexes avec la bonne architecture, des données annotées et une fonction de perte adéquate comme la segmentation sémantique ou la détection d’objets.

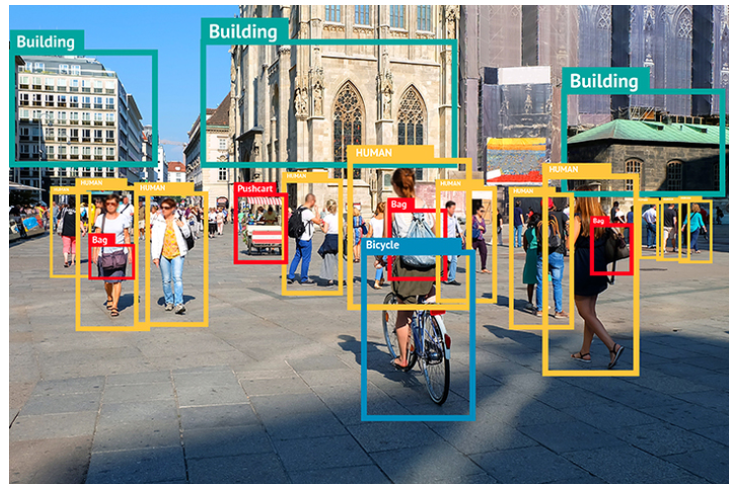
Dernières remarques

• Lorsqu’on dispose de peu de données, on peut utiliser un réseau entraîné à une tâche de classification différente pour le modifier : les premiers filtres détectent des caractéristiques assez universelles qui seront pertinentes même dans un contexte différente. Ce procédé s’appelle transfer learning.

• On a réussi à adapter la structure des réseaux de neurones de base pour les images afin de tenir compte de l’agencement spatial des pixels. Il existe une variante pour traiter les objets organisés sous forme séquentielle : le texte, un signal sonore ou n’importe quel données organisées en suite de longueur variable, ce sont les Réseaux de Neurones Récurrents ou Reccurent Neural Network (RNN).

• Il est même possible de combiner les deux architectures Recurrent Convolutional Neural Network pour analyser des vidéos.